Método de Newton

O Método de Newton é um conhecido algoritmo para chegar a soluções númericas de uma equação, normalmente uma para a qual a solução não é tão trivial.

Por exemplo, imagine que queiramos encontrar encontrar a raiz da função quadrática $x = \sqrt{5} \Rightarrow x^2 = 5 \Rightarrow x^2 - 5 = 0$. Como poderíamos fazer isso?

Newton criou um método (verdadeiramente um algoritmo) extraordinariamente eficiente para chegar à solução, em que se faz uso de seus estudos em cálculo diferencial.

Calcular $\sqrt{5}$, hoje em dia, é trivial, basta qualquer calculadora. Mas, como será que a calculadora faz esse cálculo? Talvez seja esse o algoritmo que ela mesma usa. Vamos entender como isso funciona então.

Para melhor entendimento do problema, vejamos o gráfico da função antes.

%matplotlib inlineimport matplotlib.pyplot as pltimport seaborn as snsimport numpy as np sns.set() def f(x): return x**2 - 5X = np.linspace(-5, 5, 500) plt.plot(X, f(X))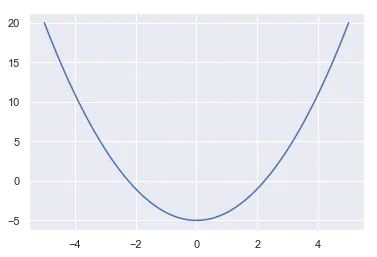

Podemos verificar que ela intercepta o eixo x quando $x$ é um pouquinho acima de 2, quer dizer, quando $x = \sqrt{5} \approx 2.23$.

Ok, mas como chegamos até ali com cálculo diferencial? O raciocínio é como segue: vamos fazer uma estimativa inicial, um valor que achamos que seja próximo da solução. Por exemplo, 1.

Com esse valor, a ideia é obter a reta tangente àquele ponto, o que é algo muito mais fácil de lidar. E, para isso, é claro que precisamos calcular $f^{'}(1)$, a inclinação dessa reta naquele ponto.

E, com ela em mãos, queremos achar onde essa reta intercepta o eixo x, e este deve ser um ponto mais próximo da raiz, mas não exatamente a raiz. Isto porque estamos calculando a raiz de uma reta pra nos aproximarmos da raiz de uma parábola, que não é linear, é claro.

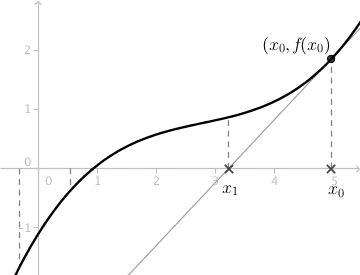
Até então, o método não parece tão impressionante. Mas e se fizermos isso de novo, usando como estimativa a raiz dessa reta? Acontece que se repetirmos esse processo algumas vezes mais podemos chegar numa estimativa muito próxima da solução.

Aproximação Linear

Esse uso da reta tangente é o que se conhece por aproximação linear. Por exemplo, retomando a função quadrática. A derivada dela é obtida pela regra da potência, $\frac{d(x^2)}{dx} = 2x$. Já a equação da tangente é obtida simplesmente da equação de uma reta:

No nosso caso, queremos achar a reta tangente quando $x_0 = 1$, sendo $f(x_0) = x^2 - 5 = 1 - 5 = -4$. Logo, a reta que tangencia o ponto $(1, -4)$ é:

Mas, é crucial perceber que essa é a equação da reta tangente ao ponto $(x_0, y_0)$ da função f(x). Então, o que realmente podemos alegar é que, para um dado número $a$, o valor de $f(a) \approx y(a)$, quando $a \approx x_0$: a reta tangente a um dado ponto de uma função é muito próxima da própria função para valores não muito distantes do ponto.

No gráfico abaixo isso pode ser melhor visualizado. Perceba que para valores próximos de 1, a reta tangente está bem próxima da parábola, mas vai ficando cada vez mais distante quando x se afasta de 1. E é esse o sentido de uma aproximação linear.

def tang(x):    return 2 * x - 6  plt.plot(X, f(X), label=r"$x^2 - 5$")plt.plot(X, tang(X), label=r"$2x - 6$")plt.xlim(-0.5, 3.5)plt.legend()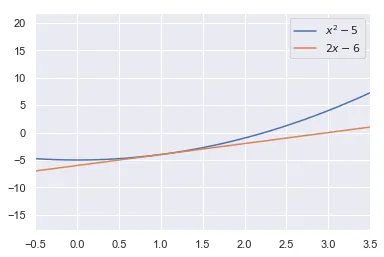

Nesse zoom, também podemos ver que a reta tangente ao ponto $(1, -4)$ cruza o eixo $x$ um pouco mais adiante de $2.23$. Mais especificamente, quando $2x - 6 = 0 \Rightarrow 2x = 6 \Rightarrow x = 3$.

O que é um pouco mais próximo da raiz do que a estimativa inicial 1. E é exatamente nisso que consiste o Método de Newton, em se aproximar cada vez mais da raiz de $f(x)$ usando a reta que tangencia um dado ponto desta função.

Assim, nosso objetivo fica melhor delineado dessa forma: queremos sempre o valor de $x$ da reta tangente a um ponto $(x_0, y_0)$ que faz com que $y = 0$:

Plugando os valores de nossa estimativa inicial, obtemos:

E a ideia é usarmos o 3 como um novo $x_0$, e com ele calcularmos uma nova estimativa para a raiz com a reta que tangencia $(3, 4)$.

O que já é uma ótima aproximação de $\sqrt{5}$. Abaixo um gráfico do que mais ou menos aconteceu. A função laranja é a tangente ao ponto $(1, -4)$, e a verde ao ponto $(3, 4)$. Veja como o intercepto-x da tangente a este último ponto é próximo da raiz da parábola.

def f(x):    return x ** 2 - 5  def tangente_um(x):    return 2 * x - 6  def tangente_dois(x):    return 6 * x - 14  X = np.linspace(-5, 5, 1000) plt.plot(X, f(X), label=r"$x^2 - 5$")plt.plot(X, tangente_um(X), label=r"$2x - 6$")plt.plot(X, tangente_dois(X), label=r"$6x - 14$") plt.hlines(0, -1, 4, "grey", "dashed")plt.vlines(3, -10, 10, "grey", "dashed") plt.xlim(-1, 4)plt.ylim(-10, 10)plt.legend()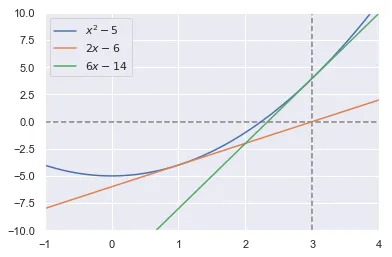

Seria interessante escrevermos uma função para fazer esses cálculos, e ela inevitavelmente teria que lidar com cálculo diferencial. Para isso, existe uma biblioteca que pode nos ajudar.

Introduzindo SymPy

Essa biblioteca fornece suporte para trabalhar com álgebra simbólica. Nela contamos com funções para calcular limites, derivadas, integrais, expandir polinômicos, simplificar expressões etc.

Por exemplo, se quisermos calcular a derivada da função $x^2 - 5$.

from sympy import symbols, diff, limit, integrate, oo x = symbols("x") diff(x ** 2 - 5)

2*x

Podemos também calcular limites, por exemplo $\lim\_{x \to \infty} \frac{1}{x} = 0$

limit(1 / x, x, oo)

0

Ou mesmo integrais indefinidas, $\int x^2 , dx = \frac{x^3}{3} + c$

integrate(x ** 2)

x**3/3

A função assim como está não serve para retornar qualquer valor, ela praticamente só aceita funções do próprio SymPy. Para a utilizarmos como uma função qualquer, devemos usar lambdify(). Para nossos objetivos, essa última e a função diff serão suficientes.

Um código para o algoritmo

Antes de apresentar a função em si, melhor explicar como eu a pensei.

Primeiramente, ela tomará três argumentos: a função, o valor para o qual queremos uma solução, e a estimativa inicial. Por exemplo, no nosso caso, ela tomaria os argumentos $x^2$, $5$ e $1$.

Em seguida, construirei simbolicamente, com estes argumentos, nossa $f(x)$ e sua derivada, $f'(x)$. E com isso temos tudo que precisamos para executarmos o método.

No algoritmo, decidi por 5 iterações, printando três colunas com os resultados a cada iteração: a estimativa inicial, a nova estimativa e, por fim, a diferença entre as duas, a fim de verificar como a cada iteração o valor de x se aproxima mais do da raiz.

from sympy.utilities.lambdify import lambdify  def newton(funcao, numero, estimativa):    f = lambdify(x, funcao - numero)  # x^2 - 5    df = lambdify(x, diff(funcao - numero))  # 2x     print("est.    | nova est. | diferença")     for _ in range(5):        nova_est = estimativa - f(estimativa) / df(estimativa)        print(            f"{estimativa:.5f} | {nova_est:^ 9.5f} | {abs(nova_est - estimativa):.20f}"        )        estimativa = nova_est     return estimativa  print(f"\nO quanto erramos: {abs(np.sqrt(5) - newton(x**2, 5, 1))}")

est.    | nova est. | diferença1.00000 |  3.00000  | 2.000000000000000000003.00000 |  2.33333  | 0.666666666666666518642.33333 |  2.23810  | 0.095238095238095343832.23810 |  2.23607  | 0.002026342451874718622.23607 |  2.23607  | 0.00000091814338532004O quanto erramos: 1.8829382497642655e-13

E assim vemos que o erro foi desprezível.

A vantagem de usar o SymPy é que agora podemos estimar a raiz de qualquer tipo de função. Por exemplo, a raiz cúbica de 5, ou algo mais complicado:

print(f"\nO quanto erramos: {abs(5**(1/3) - newton(x**3, 5, 2))}")

est.    | nova est. | diferença2.00000 |  1.75000  | 0.250000000000000000001.75000 |  1.71088  | 0.039115646258503389281.71088 |  1.70998  | 0.000907924824521844091.70998 |  1.70998  | 0.000000482240141819191.70998 |  1.70998  | 0.00000000000013589130O quanto erramos: 2.220446049250313e-16

Uma das raízes para função $x^4 + x^3 - x^2 - 5$ deve ser:

newton(x ** 4 + x ** 3 - x ** 2, 5, 1)

est.    | nova est. | diferença1.00000 |  1.80000  | 0.800000000000000044411.80000 |  1.52529  | 0.274707959793534461921.52529 |  1.43509  | 0.090202365878929713361.43509 |  1.42600  | 0.009089438495259782871.42600 |  1.42591  | 0.000086811266254427371.4259134245660217

Se plotarmos seu gráfico, veremos que esse é um valor razoável. Uma raiz parece estar entre 1 e 2, e foi a que achamos. E uma outra está muito próxima de -2.

X = np.linspace(-5, 5, 1000)  def g(x):    return x ** 4 + x ** 3 - x ** 2 - 5  plt.plot(X, g(X))plt.hlines(0, -5, 5, color="grey")plt.xlim(-5, 5)plt.ylim(-7.5, 5)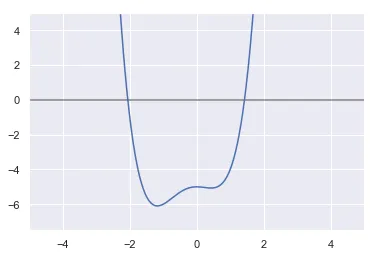

Vamos tentar achar essa outra raiz com nossa função. Para isso, basta mudarmos nossa estimativa inicial de forma a nos aproximarmos daquela outra raiz.

newton(x ** 4 + x ** 3 - x ** 2, 5, -1.5)

est.    | nova est. | diferença-1.50000 | -2.98333  | 1.48333333333333339255-2.98333 | -2.45626  | 0.52707184463468736979-2.45626 | -2.16542  | 0.29084549734551234934-2.16542 | -2.06890  | 0.09651451804451394167-2.06890 | -2.05885  | 0.01005450745933744727-2.0588469658492823

Limitações do método

Essa é uma função complicadinha e expõe algumas limitações do método que Newton criou. Por exemplo, imagine que usemos como estimativa um valor próximo de um mínimo, digamos que 0.5.

newton(x ** 4 + x ** 3 - x ** 2, 5, 0.5)

est.    | nova est. | diferença0.50000 |  20.75000 | 20.2500000000000000000020.75000 |  15.50807 | 5.2419317874583892802315.50807 |  11.57934 | 3.9287282396012521701311.57934 |  8.63653  | 2.942806536150184726358.63653 |  6.43473  | 2.201800350625481073056.434733086164693

O resultado foi bem catastrófico. É claro, não poderíamos esperar que ele fosse infalível. Vejamos as razões pelas quais ele pode falhar.

Primeiro, é muito claro que o resultado final a que chegaremos depende da estimativa inicial. Logo, se fizermos uma estimativa desarrazoada, é muito provável que não cheguemos a uma solução pertinente.

Além disso, a derivada da função naquele ponto não deve ser muito pequena. No limite, se ela for zero, teremos uma indefinição, uma divisão por zero.

E se ela for muito pequena, a reta tangente será muito pouco inclinada e jogará a estimativa para muito longe da raiz. E foi isso o que aconteceu ali em cima. Por exemplo, consideremos a função $x^3 - x$.

X = np.linspace(-2, 2, 1000) plt.plot(X, X ** 3 - X)plt.hlines(0, -5, 5, color="grey")plt.xlim(-2, 2)plt.ylim(-0.5, 0.5)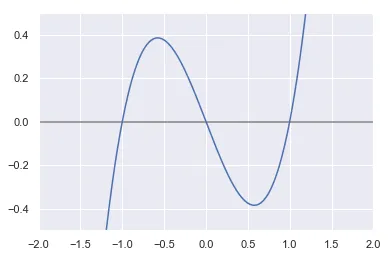

Pelo gráfico, salta à vista que as três raízes são 0, 1 e -1. Ok, mas imagine que queiramos estimar a raiz não-nula positiva com este método.

Não poderíamos escolher 0.5 como estimativa, porque isso nos jogaria para o outro lado e acabaríamos achando algo próximo da raiz negativa:

newton(x ** 3 - x, 1, 0.5)

est.    | nova est. | diferença0.50000 | -5.00000  | 5.50000000000000000000-5.00000 | -3.36486  | 1.63513513513513508713-3.36486 | -2.28096  | 1.08390981119991192116-2.28096 | -1.55628  | 0.72467848569769000022-1.55628 | -1.04351  | 0.51277134078822550478-1.0435052271790375

E se escolhêssemos algo muito perto do mínimo, aquele mesmo fiasco aconteceria.

newton(x ** 3 - x, 1, 0.6)

est.    | nova est. | diferença0.60000 |  17.90000 | 17.2999999999999829469717.90000 |  11.94680 | 5.9531976713912229115511.94680 |  7.98552  | 3.961281976672553994947.98552 |  5.35691  | 2.628611037140749395755.35691 |  3.62500  | 1.731913281849362107323.624996032946096

Como esperado, a tangente ali é pouquíssimo inclinada, e jogou a estimativa para muito longe, tanto que em 5 tentativas não conseguimos uma estimativa muito boa. Veja o gráfico.

X = np.linspace(-2, 2, 1000) plt.plot(X, X ** 3 - X, label=r"$x^3 - x$")plt.plot(X, -0.432 + 0.08 * X, label=r"$-0.432 + 0.08x$") plt.hlines(0, -5, 5, color="grey")plt.xlim(-2, 2)plt.ylim(-0.5, 0.5)plt.legend()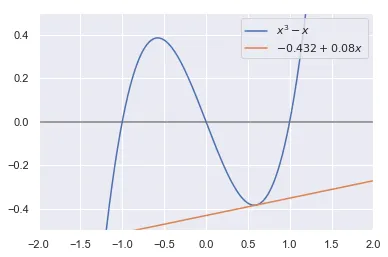

Conclusões

O interessante desse algoritmo é ser uma aplicação de cálculo diferencial. É bastante simples sem sacrificar o lado da eficiência, mas também vimos que há certas limitações. É claro, ele não poderia fazer milagres. Mas, hoje em dia, basta plotar o gráfico em questão para ter uma ideia de onde estão as raízes, como acabamos de fazer aqui com a ajuda do matplotlib.